Matrix Tree

https://en.wikipedia.org/wiki/Kirchhoff's_theorem

4 5
1 3
1 4
2 3
2 4
3 4

2 0 -1 -1
0 2 -1 -1
-1 -1 3 -1
-1 -1 -1 3

2 0 -1
0 2 -1
-1 -1 3

223 - 2 - 2 = 8

Matrix-Tree Theorem

无向图是有向图的一个特殊情况

有向图
a[i][j] = 边数的相反数 (i!=j)
a[i][j] = 入度 (i==j)

The BEST Theorem

可以结合Matrix-Tree Theorem计算有向图的欧拉回路个数

P6178 【模板】Matrix-Tree 定理

https://www.luogu.com.cn/problem/P6178

题目描述

给定一张 $n$ 个结点 $m$ 条边的带权图（可能为无向图，可能为有向图）。

定义其一个生成树 $T$ 的权值为 $T$ 中所有边权的乘积。

求其所有不同生成树的权值之和，对 $10^9+7$ 取模。

---

注意：

1. 本题中，有向图的生成树指的是 以 $1$ 为根的外向树；

2. 两棵生成树 $T_1,T_2$ 不同，当且仅当存在存在一条边 $e$，满足 $e\in T_1,\ \ e\notin T_2$。

输入格式

第一行：三个整数 $n,m,t$，分别表示图的结点数量，边的数量和图的类型（$t=0$ 时为无向图，$t=1$ 时为有向图）。

接下来 $m$ 行：每行三个整数 $u,v,w$。

如果 $t=0$，表示 $u,v$ 之间有一条权值为 $w$ 的无向边；

如果 $t=1$，表示从 $u$ 到 $v$ 有一条权值为 $w$ 的有向边。

输出格式

第一行：一个整数 $ans$，表示给定的图的生成树权值和对 $10^9+7$ 取模的结果。

样例 #1

样例输入 #1

5 8 0
2 3 1
1 2 3
4 5 1
4 2 2
3 5 2
3 4 3
3 4 1
3 3 5

样例输出 #1

144

样例 #2

样例输入 #2

5 9 1
1 2 3
3 2 1
1 3 1
2 4 2
3 5 1
4 3 4
3 5 1
5 4 1
4 4 6

样例输出 #2

72

提示

【样例 $1$ 解释】

样例 $1$ 中的无向图如左图所示：

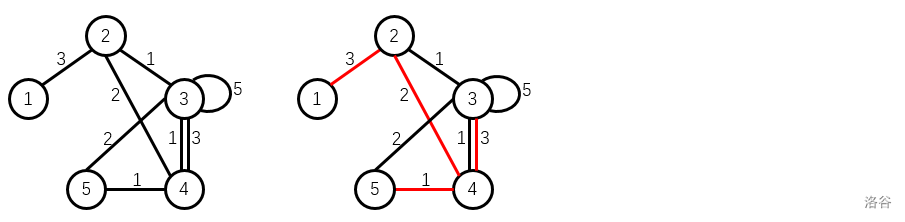
右图为其一个权值为 $3\times 1\times 2\times 3=18$ 的生成树的例子。

---

【样例 $2$ 解释】

样例 $2$ 中的有向图如左图所示：

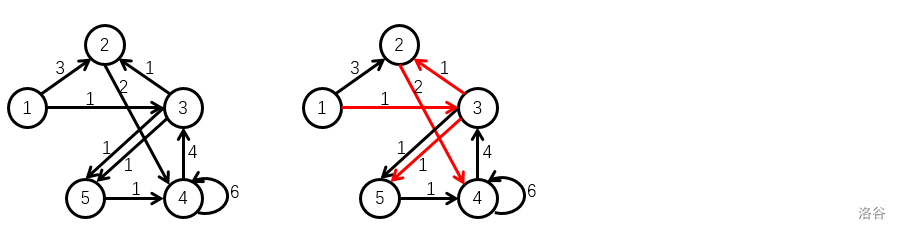
右图为其一个权值为 $1\times 1\times 1\times 2=2$ 的生成树（以 $1$ 为根的外向树）的例子。

---

【数据范围】

对于 $100\%$ 的数据：$1\leq n\leq 300,\ \ 1\leq m\leq 10^5,\ \ t\in \{0,1\},\ \ 1\leq u,v\leq n,\ \ 1\leq w\leq 10^9$。

对于测试点 $1,2,3,4,5,6$，$t=0$；对于测试点 $7,8,9,10,11$，$t=1$。

图中 可能 存在重边和自环，重边算作多条边。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int mod = 1000000007;
int n, m, t, u, v, w;
int a[300][300];
int work()
{
	int ans = 1;
	for (int i = 1; i < n; i++)
	{
		for (int j = i + 1; j < n; j++)
		{
			while (a[j][i])
			{
				int t = a[i][i] / a[j][i];
				for (int k = 1; k < n; k++)
				{
					a[i][k] = (a[i][k] - (long long)a[j][k] * t) % mod;
				}
				swap(a[i], a[j]);
				ans = -ans;
			}
		}
		ans = (long long)ans * a[i][i] % mod;
	}
	return (ans + mod) % mod;
}
int main()
{
	scanf("%d%d%d", &n, &m, &t);
	for (int i = 0; i < m; i++)
	{
		scanf("%d%d%d", &u, &v, &w);
		u--;
		v--;
		a[u][v] = (a[u][v] + mod - w) % mod;
		a[v][v] = (a[v][v] + w) % mod;
		if (!t)
		{
			a[v][u] = (a[v][u] + mod - w) % mod;
			a[u][u] = (a[u][u] + w) % mod;
		}
	}
	printf("%d\n", work());
	return 0;
}

题解

P4455 [CQOI2018]社交网络

https://www.luogu.com.cn/problem/P4455

题目背景

当今社会，在社交网络上看朋友的消息已经成为许多人生活的一部分。通常，一个用户在社交网络上发布一条消息后，他的好友们也可以看见这条消息，并可能转发。转发的消息还可以继续被人转发，进而扩散到整个社交网络中。

题目描述

在一个实验性的小规模社交网络中我们发现，有时一条热门消息最终会被所有人转发。为了研究这一现象发生的过程，我们希望计算一条消息所有可能的转发途径有多少种。为了编程方便，我们将初始消息发送者编号为 $1$，其他用户编号依次递增。

该社交网络上的所有好友关系是已知的，也就是说对于 $a, b$ 两个用户，我们知道 $a$ 用户可以看到 $b$ 用户发送的消息。注意可能存在单向的好友关系，即 $a$ 能看到 $b$ 的消息，但 $b$ 不能看到 $a$ 的消息。

还有一个假设是，如果某用户看到他的多个好友转发了同一条消息，他只会选择从其中一个转发，最多转发一次消息。从不同好友的转发，被视为不同的情况。

如果用箭头表示好友关系，下图展示了某个社交网络中消息转发的所有可能情况。（初始消息是用户 $1$ 发送的，加粗箭头表示一次消息转发）

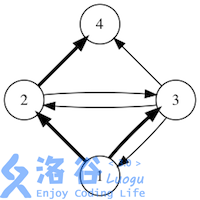
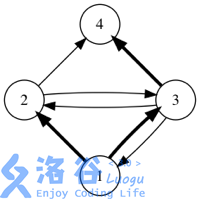
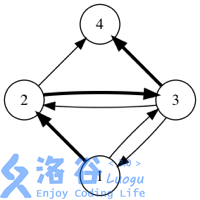
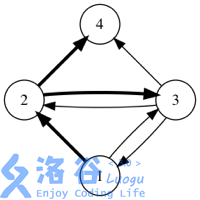
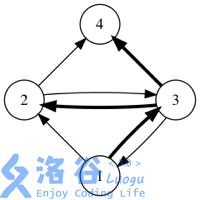
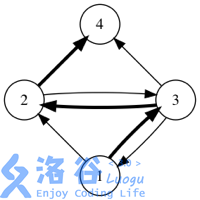
答案对 $10^4 + 7$ 取模。

输入格式

第一行有一个整数，表示用户的数量 $n$。
第二行有一个整数，表示好友关系数目 $m$。
接下来 $m$ 行，每行两个整数 $a, b$，表示一组好友关系，即用户 $a$ 可以看到用户 $b$ 发送的信息。

输出格式

输出一行一个整数表示答案对 $10^4 + 7$ 取模的结果。

样例 #1

样例输入 #1

4
7
2 1
3 1
1 3
2 3
3 2
4 3
4 2

样例输出 #1

6

提示

数据规模与约定

• 对于 $30\%$ 的数据，保证 $n \leq 10$。
• 对于 $100\%$ 的数据，保证 $1 \leq n \leq 250$，$1 \leq m \leq n \times (n - 1)$，$1 \leq a, b \leq n$。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int mod = 10007;
int n, m, u, v;
int a[300][300];
int work()
{
	int ans = 1;
	for (int i = 1; i < n; i++)
	{
		for (int j = i + 1; j < n; j++)
		{
			while (a[j][i])
			{
				int t = a[i][i] / a[j][i];
				for (int k = 1; k < n; k++)
				{
					a[i][k] = (a[i][k] - (long long)a[j][k] * t) % mod;
				}
				swap(a[i], a[j]);
				ans = -ans;
			}
		}
		ans = (long long)ans * a[i][i] % mod;
	}
	return (ans + mod) % mod;
}
int main()
{
	scanf("%d%d", &n, &m);
	for (int i = 0; i < m; i++)
	{
		scanf("%d%d", &v, &u);
		u--;
		v--;
		a[u][v]--;
		a[v][v]++;
	}
	printf("%d\n", work());
	return 0;
}

题解