矩阵乘法快速幂优化线性递推

简介

https://en.wikipedia.org/wiki/Matrix_multiplication

信息学中遇到的矩阵，可以认为都是方阵。
（在极少数情况下还是有非方阵的情况）

为了体现出矩阵乘法的效率，往往需要和快速幂结合起来使用。
因为运算结果可能很大，所以往往需要对一个数字取模

输入一个图，输入起点，问有多少个长度为k的路径

输入一个二分图，左边10个点，右边100000个点，输入起点，问有多少个长度为k的路径

矩阵乘法

对于两个 $n \times n$ 的矩阵 $A, B$ 可以定义矩阵乘法：
$C_{i, j} = \sum_{k = 1}^n A_{i, k} B_{k, j}$
这样定义出的矩阵乘法，满足结合律，可以使用快速幂来计算矩阵乘法。

一般情况下，为了计算不越界，都会要求对某个数字取模。

void mul(int a[100][100], int b[100][100])
{
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < m; j++) {
            for (int k = 0; k < m; k++) {
                c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % p;
            }
        }
    }
}

如果a[][]是一个行向量而不是矩阵，可以用以下的方式常数优化。

for (int i = 0; i < m; i++) {
    for (int k = 0; k < m; k++) {
        if (a[i][k] == 0) {
            continue;
        }
        for (int j = 0; j < m; j++) {
            c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % p;
        }
    }
}

如果b矩阵的零多，应该先枚举j和k然后如果b[k][j]是0，就跳过枚举i的循环

Fibonacci数

#include <bits/stdc++.h>
using namespace std;
const int m = 2;
int a[m][m], b[m][m];
int n, p = 10000;
void mul(int a[m][m], int b[m][m]) {
    // a = a * b;
    int c[m][m] = {};
    for (int i = 0; i < m; i++) {
        for (int j = 0; j < m; j++) {
            for (int k = 0; k < m; k++) {
                c[i][j] = (c[i][j] + a[i][k] * b[k][j]) % p;
            }
        }
    }
    memcpy(a, c, sizeof c); // 不能写sizeof a
}
int main() {
    a[0][1] = 1;
    b[0][1] = b[1][0] = b[1][1] = 1;
    cin >> n;
    for(; n > 0; n >>= 1) {
        if (n & 1) {
            mul(a, b);
        }
        mul(b, b);
    }
    cout << a[0][0] << endl;
    return 0;
}

也可以利用Fibonacci数的性质
$F_{n + 2} = F_{n + 1} + F_{n}$
$F_{2n + 1} = F^2_{n + 1} + F^2_{n}$
$F_{2n} = (2F_{n + 1} - F_n) F^2_{n}$

这样就可以从 $(F_{n}, F_{n + 1})$ 计算出 $(F_{n+1}, F_{n+2})$ 。
也可以从 $(F_{n}, F_{n + 1})$ 计算出 $(F_{2n}, F_{2n+1})$ 。
然后就可以递归进行计算。

// F(n) 返回 make_pair(f[n], f[n+1])
LL F(ll n)
{
    if(n==0)
        return LL(0,1);
    else if(n&1)
    {
        LL u=F(n-1);
        return LL(u.Y,(u.X+u.Y)%p);
    }
    else
    {
        LL u=F(n/2);
        return LL((2*u.Y+p-u.X)%p*u.X%p,(u.X*u.X+u.Y*u.Y)%p);
    }
}

参考题目

poj 3070
因为结果对 $10000$ 取模， $f_n \equiv f_{n + 15000} \pmod{15000}$
所以读入 $n$ 直接对 $15000$ 取模即可。

P1349, P1357, P1707, P1939, P1962, P2044, P2461, P3746, P4599, P4910, P5004

P2151 [SDOI2009] HH去散步

https://www.luogu.com.cn/problem/P2151

题目描述

HH有个一成不变的习惯，喜欢饭后百步走。所谓百步走，就是散步，就是在一定的时间内，走过一定的距离。但是同时HH又是个喜欢变化的人，所以他不会立刻沿着刚刚走来的路走回。又因为HH是个喜欢变化的人，所以他每天走过的路径都不完全一样，他想知道他究竟有多少种散步的方法。

现在给你学校的地图（假设每条路的长度都是一样的都是1），问长度为t，从给定地点A走到给定地点B共有多少条符合条件的路径

输入格式

第一行：五个整数N，M，t，A，B。其中N表示学校里的路口的个数，M表示学校里的路的条数，t表示HH想要散步的距离，A表示散步的出发点，而B则表示散步的终点。

接下来M行，每行一组Ai，Bi，表示从路口Ai到路口Bi有一条路。数据保证Ai != Bi，但不保证任意两个路口之间至多只有一条路相连接。路口编号从0到N - 1。同一行内所有数据均由一个空格隔开，行首行尾没有多余空格。没有多余空行。答案模45989。

输出格式

一行，表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

对于30%的数据，N ≤ 4，M ≤ 10，t ≤ 10。

对于100%的数据，N ≤ 50，M ≤ 60，t ≤ 2^30，0 ≤ A,B

参考代码

#include <bits/stdc++.h>
using namespace std;
const int p = 45989;
int n, m, t, s, e, x, y;
int a[120][120];
int b[120][120];
void mul(int a[120][120], int b[120][120])
{
	int w[120][120] = {};
	for (int i = 0; i < m; i++)
	{
		for (int k = 0; k < m; k++)
		{
			if (a[i][k] == 0)
			{
				continue;
			}
			for (int j = 0; j < m; j++)
			{
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
vector<int> in[60], ot[60];
int main()
{
	scanf("%d%d%d%d%d", &n, &m, &t, &s, &e);
	for (int i = 0; i < m; i++)
	{
		scanf("%d%d", &x, &y);
		ot[x].push_back(i);
		in[y].push_back(i);
		ot[y].push_back(i + m);
		in[x].push_back(i + m);
	}
	for (int i = 0; i < n; i++)
	{
		for (int j: in[i])
		{
			for (int k: ot[i])
			{
				if (j - k != m && k - j != m)
				{
					b[j][k] = 1;
				}
			}
		}
	}
	m *= 2;
	for (int j: ot[s])
	{
		a[0][j] = 1;
	}
	for (t--; t > 0; t >>= 1)
	{
		if (t & 1)
		{
			mul(a, b);
		}
		mul(b, b);
	}
	int z = 0;
	for (int j: in[e])
	{
		z = (z + a[0][j]) % p;
	}
	printf("%d\n", z);
	return 0;
}

题解

P3169 [CQOI2015]多项式

https://www.luogu.com.cn/problem/P3169

题目描述

在学习完二项式定理后，数学老师给出了一道题目：已知整数 $n,t$ 和 $a_k$ （ $0\le k\le n$ ），求 $b_k$ （ $0\le k\le n$ ）的表达式使得:

$\sum_{k=0}^n a_kx^k=\sum_{k=0}^nb_k(x-t)^k$

同学们很快算出了答案。见大家这么快就搞定了，老师便布置了一个更 BT 的作业：计算某个 $b_k$ 的具体数值！接着便在黑板上写下了 $n,t$ 的数值，由于 $a_k$ 实在太多，不能全写在黑板上，老师只给出了一个 $a_k$ 的递推式，让学生自行计算:

$a_k= \begin{cases} (1234\cdot a_{k-1}+5678)\bmod 3389 & k\gt 0 \\ 1 & k=0 \\ \end{cases}$

正在学习信息竞赛的你觉得这个作业实在不适合手工完成，便敲起了代码……

输入格式

输入文件共三行，第一行为一个正整数 $n$ ，第二行为一个非负整数 $t$ ，第三行为一个非负整数 $m$ 。

输出格式

输出一行，为 $b_m$ 的值。

样例 #1

样例输入 #1

3
2
2

样例输出 #1

提示

数据范围：

对于 $20\%$ 的数据， $t=0$ 。

对于另外 $30\%$ 的数据， $n\le 10^5$ 。

对于 $100\%$ 的数据， $0\lt n\le 10^{3000}$ ， $0\le t\le 10^4$ ， $0\le n-m\le 5$ 。

参考代码

题解

P3193 [HNOI2008]GT考试

https://www.luogu.com.cn/problem/P3193

题目描述

阿申准备报名参加 GT 考试，准考证号为 $N$ 位数 $X_1,X_2…X_n(0\le X_i\le9)$ ，他不希望准考证号上出现不吉利的数字。
他的不吉利数字 $A_1,A_2…A_m(0\le A_i\le 9)$ 有 $M$ 位，不出现是指 $X_1,X_2…X_n$ 中没有恰好一段等于 $A_1,A_2…A_m$ ， $A_1$ 和 $X_1$ 可以为 $0$

输入格式

第一行输入N,M,K.接下来一行输入M位的数。

输出格式

阿申想知道不出现不吉利数字的号码有多少种，输出模 $K$ 取余的结果。

样例 #1

样例输入 #1

4 3 100
111

样例输出 #1

提示

$N\leq10^9,M\leq20,K\leq1000$

参考代码

#include <bits/stdc++.h>
using namespace std;
int n, m, p, z;
int a[30][30];
int b[30][30];
string s;
void mul(int a[30][30], int b[30][30])
{
	int w[30][30] = {};
	for (int i = 0; i < m; i++)
	{
		for (int j = 0; j < m; j++)
		{
			for (int k = 0; k < m; k++)
			{
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int main()
{
	cin >> n >> m >> p >> s;
	for (int i = 0, k; i < m; i++)
	{
		for (int j = '0'; j <= '9'; j++)
		{
			for (k = i + 1; k > 0; k--)
			{
				if (s.substr(0, k - 1) == s.substr(i - k + 1, k - 1) && j == s[k - 1])
				{
					break;
				}
			}
			b[i][k]++;
		}
	}
	a[0][0] = 1;
	for (; n > 0; n >>= 1)
	{
		if (n & 1)
		{
			mul(a, b);
		}
		mul(b, b);
	}
	for (int i = 0; i < m; i++)
	{
		z = (z + a[0][i]) % p;
	}
	cout << z << endl;
	return 0;
}

题解

P3597 [POI2015] WYC

https://www.luogu.com.cn/problem/P3597

题目描述

给定一张 $n$ 个点 $m$ 条边的带权有向图，每条边的边权只可能是 $1$ ， $2$ ， $3$ 中的一种。

将所有可能的路径按路径长度排序，请输出第 $k$ 小的路径的长度，注意路径不一定是简单路径，即可以重复走同一个点。

输入格式

第一行包含三个整数 $n,m,k$ （ $1\le n\le 40$ ， $1\le m\le 1000$ ， $1\le k\le 10^{18}$ ）。

接下来 $m$ 行，每行三个整数 $u,v,c$ （ $1\leq u,v\leq n$ ， $u\neq v$ ， $1\le c\le 3$ ），表示从 $u$ 出发有一条到 $v$ 的单向边，边长为 $c$ 。

可能有重边。

输出格式

包含一行一个正整数，即第 $k$ 短的路径的长度，如果不存在，输出 $-1$ 。

样例 #1

样例输入 #1

样例输出 #1

提示

【样例解释】

长度为 $1$ 的路径有 $1\to 2$ ， $5\to 3$ ， $4\to 5$ 。长度为 $2$ 的路径有 $2\to3$ ， $3\to4$ ， $4\to5\to3$ 。长度为 $3$ 的路径有 $4\to6$ ， $1\to2\to3$ ， $3\to4\to5$ ， $5\to3\to4$ 。长度为 $4$ 的路径有 $5\to3\to4\to5$ 。

原题名称：Wycieczki。

参考代码

题解

P3758 [TJOI2017]可乐

https://www.luogu.com.cn/problem/P3758

题目描述

加里敦星球的人们特别喜欢喝可乐。因而，他们的敌对星球研发出了一个可乐机器人，并且放在了加里敦星球的 $1$ 号城市上。这个可乐机器人有三种行为：停在原地，去下一个相邻的城市，自爆。它每一秒都会随机触发一种行为。现在给加里敦星球城市图，在第 $0$ 秒时可乐机器人在 $1$ 号城市，问经过了 $t$ 秒，可乐机器人的行为方案数是多少？

输入格式

第一行输入两个正整数 $N$ ， $M$ 。 $N$ 表示城市个数， $M$ 表示道路个数。

接下来 $M$ 行每行两个整数 $u$ ， $v$ ，表示 $u$ ， $v$ 之间有一条道路。保证两座城市之间只有一条路相连，且没有任何一条道路连接两个相同的城市。

最后一行是一个整数 $t$ ，表示经过的时间。

输出格式

输出可乐机器人的行为方案数，答案可能很大，请输出对 $2017$ 取模后的结果。

样例 #1

样例输入 #1

样例输出 #1

提示

样例输入输出 1 解释

$1$ ->爆炸。
$1$ -> $1$ ->爆炸。
$1$ -> $2$ ->爆炸。
$1$ -> $1$ -> $1$ 。
$1$ -> $1$ -> $2$ 。
$1$ -> $2$ -> $1$ 。
$1$ -> $2$ -> $2$ 。
$1$ -> $2$ -> $3$ 。

数据范围与约定

对于 $20\%$ 的数据，保证 $t \leq 1000$ 。
对于 $100\%$ 的数据，保证 $1 < t \leq 10^6$ ， $1 \leq N \leq30$ ， $0 < M < 100$ ， $1 \leq u, v \leq N$ 。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int p = 2017;
int n, m, t, x, y;
void mul(int a[31][31], int b[31][31])
{
	int w[31][31] = {};
	for (int i = 0; i <= n; i++)
	{
		for (int j = 0; j <= n; j++)
		{
			for (int k = 0; k <= n; k++)
			{
				w[i][j] = (w[i][j] + a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int a[31][31];
int b[31][31];
int main() {
	cin >> n >> m;
	for (int i = 0; i < m; i++)
	{
		cin >> x >> y;
		b[x][y] = 1;
		b[y][x] = 1;
	}
	for (int i = 0; i <= n; i++)
	{
		a[i][i] = 1;
		b[i][i] = 1;
		b[i][0] = 1;
	}
	cin >> t;
	for (t++; t > 0; t >>= 1)
	{
		if (t & 1)
		{
			mul(a, b);
		}
		mul(b, b);
	}
	cout << a[1][0] << endl;
	return 0;
}

题解

P3990 [SHOI2013]超级跳马

https://www.luogu.com.cn/problem/P3990

题目描述

现有一个 $n$ 行 $m$ 列的棋盘，一只马欲从棋盘的左上角跳到右下角。每一步它向右跳奇数列，且跳到本行或相邻行。跳越期间，马不能离开棋盘。例如，当 $n = 3$ ， $m = 10$ 时，下图是一种可行的跳法。

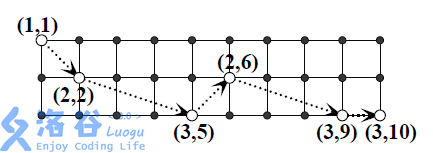
试求跳法种数对 $30\,011$ 取模的结果。

输入格式

仅有一行，包含两个正整数 $n, m$ ，表示棋盘的规模。

输出格式

仅有一行，包含一个整数，即跳法种数模 $30\,011$ 后的结果。

样例 #1

样例输入 #1

3 5

样例输出 #1

提示

对于 $10\%$ 的数据， $1 \leq n \leq 10$ ， $2 \leq m \leq 10$ ；
对于 $50\%$ 的数据， $1 \leq n \leq 10$ ， $2 ≤ m ≤ 10^5$ ；
对于 $80\%$ 的数据， $1 \leq n \leq 10$ ， $2 \leq m \leq 10^9$ ；
对于 $100\%$ 的数据， $1 \leq n \leq 50$ ， $2 \leq m \leq 10^9$ 。

参考代码

题解

P5392 [Cnoi2019]雪松树之约

https://www.luogu.com.cn/problem/P5392

题目背景

由于Cirno突然犯懒, 所以背景故事咕咕咕了。

题目描述

Cirno 定义了一种图：圆柱网络 $G( L, x )$ 。

$G(L, x)$ 表示一个有 $L \times x$ 个节点的图。

其中每个节点用一个整数二元组 $( a, b )$ 表示 $( 1 \le a \le L, 1 \le b \le x )$ 。

对于 $\forall i \in (1,L], \ j \in (0,x]$ , 节点 $(i, j)$ 与节点 $(i - 1, j)$ 之间有一条边。

对于 $\forall i \in [1,L], \ j \in (0,x)$ , 节点 $(i, j)$ 与节点 $(i, j +1)$ 之间有一条边。

对于 $\forall i \in [1,L]$ 节点 $(i, x)$ 与节点 $(i, 1)$ 之间有一条边。

现在 Cirno 想知道 $G( L, x )$ 的 独立集 的个数。

由于你不会高精度，所以你需要将答案对 $998244353$ 取模。

输入格式

一行，两个整数, L, x。

输出格式

一行，一个整数，表示 $G(L,x)$ 的独立集的个数对 $998244353$ 取模后的结果。

样例 #1

样例输入 #1

3 4

样例输出 #1

样例 #2

样例输入 #2

1000 8

样例输出 #2

124141757

提示

对于前 10% 的数据 $L, x \le 8$

对于前 30% 的数据 $x \le 8$

对于前 50% 的数据 $x \le 11$

对于 100% 的数据 $0 < L \le 10^{18}, 0 <x \le 17$

本题采用捆绑测试.

下图是 $G( 3, 4 )$ 的示例图.

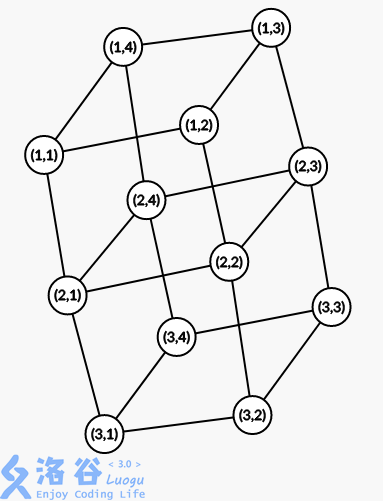
参考代码

题解

P5517 [MtOI2019]幻想乡数学竞赛

https://www.luogu.com.cn/problem/P5517

题目背景

一年一度的幻想乡数学竞赛 (thMO) 又要开始了。

幻想乡中学习数学的少 (lao) 女 (tai) 们 (po) 和冰之妖精 baka 一起准备着 thMO。

但是在那一刻，幻想乡日复一日的宁静被打破了。

广播里，播放起了死亡的歌曲！

在那一刻，人们又回想起了被算数支配的恐惧。

就剩下 baka，baka，baka，baka 的声音在幻想乡里回荡。

河城荷取 (Kawashiro Nitori) 正坐在 thMO2019 的考场上！
因为荷取有着她的超级计算机，在成功地用光学迷彩覆盖了计算机之后，荷取在 thMO2019 的考场上所向披靡。

荷取用她的超级计算机 $0 \,\mathrm{ms}$ 跑出了这么一道题：
- $\exists \{ a_n\} (n=0,1,\cdots ,10^{18})$ ，已知 $a_0=2,a_1=5,a_{n+2}=3a_{n+1}-2a_n$ ，求 $a_n\bmod 10^{9}+7$
荷取：显然，这个题可以用矩阵乘法 + 快速幂，可以 $O(\log n)$ 水过去，差不多就这样：

$\begin{bmatrix} a_n & a_{n+1} \end{bmatrix}=\begin{bmatrix} a_0 & a_1 \end{bmatrix} \times \begin{bmatrix} 3 & 1 \\ -2 & 0 \end{bmatrix}^n$

但是荷取遇到了一道她不会的题，她正在寻求你的帮助呢！

题目描述

存在一个数列 $\{ a_n\} (n\in \{ 0,1,2,\cdots ,2^{64}-1\} )$ 。
已知 $a_0=-3,a_1=-6,a_2=-12,a_n=3a_{n-1}+a_{n-2}-3a_{n-3}+3^n$ 。

现在给你一个非负整数 $n$ ，令 $p=10^{9}+7$ ，请你求出 $a_n \bmod p$ 。
注：若 $a_n<0$ ，请输出 $(a_n \bmod p+p)\bmod p$ 。

为了更充分地考验你的水平，荷取设置了 $T$ 组询问。

为了在某种程度上减少你的输入和输出量，我们采用以下的代码来生成询问：

namespace Mker
{
//  Powered By Kawashiro_Nitori
//  Made In Gensokyo, Nihon
	#include<climits>
	#define ull unsigned long long
	#define uint unsigned int
	ull sd;int op;
	inline void init() {scanf("%llu %d", &sd, &op);}
	inline ull ull_rand()
	{
		sd ^= sd << 43;
		sd ^= sd >> 29;
		sd ^= sd << 34;
		return sd;
	}
	inline ull rand()
	{
		if (op == 0) return ull_rand() % USHRT_MAX + 1;
		if (op == 1) return ull_rand() % UINT_MAX + 1; 
		if (op == 2) return ull_rand();
	}
}

在调用 Mker::init() 函数之后，你第 $i$ 次调用 Mker::rand() 函数时返回的便是第 $i$ 次询问的 $n_i$ 。

在这里给出 $op$ 的限制：

如果 $op=0$ ，满足 $n_i \leq 2^{16}$ 。
如果 $op=1$ ，满足 $n_i \leq 2^{32}$ 。
如果 $op=2$ ，满足 $n_i \leq 2^{64}-1$ 。

为了减少你的输出量，你只需要输出所有询问答案的异或和。

输入格式

第一行三个整数，输入 $T$ ， $seed$ 和 $op$ 。

输出格式

第一行一个整数，输出 $T$ 组询问的答案的异或和。

样例 #1

样例输入 #1

142857 1145141919 0

样例输出 #1

562611141

样例 #2

样例输入 #2

142857 1145141919 1

样例输出 #2

894946216

样例 #3

样例输入 #3

142857 1145141919 2

样例输出 #3

771134436

提示

子任务

png

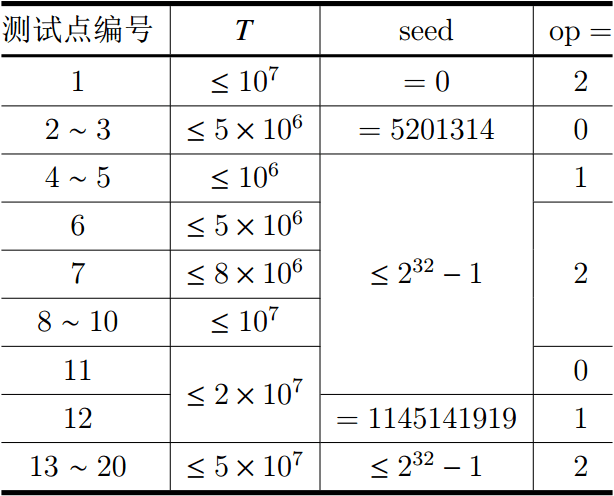
题目来源

迷途之家 2019 联赛(MtOI2019) T4

出题人：disangan233

验题人：suwakow

参考代码

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
const int mod = 1000000007;
const int inv32 = 281250002;
const int l = 65536;
ull sd;
int op;
inline ull ull_rand()
{
	sd ^= sd << 43;
	sd ^= sd >> 29;
	sd ^= sd << 34;
	return sd;
}
int t;
ull z;
ull a[l + 1];
ull b[l + 1];
int main()
{
	scanf("%d%llu%d", &t, &sd, &op);
	b[0] = a[0] = 1;
	for(int i = 0; i < l; i++)
	{
		a[i + 1] = a[i] * 3 % mod;
	}
	for(int i = 0; i < l; i++)
	{
		b[i + 1] = b[i] * a[l] % mod;
	}
	for (int tt = 0; tt < t; tt++)
	{
		ull n = ull_rand();
		if (op == 0)
		{
			n = n % USHRT_MAX + 1;
		}
		if (op == 1)
		{
			n = n % UINT_MAX + 1; 
		}
		int m = n % (mod - 1);
		z ^= ((n % mod * 36 - 117 + mod) % mod * b[m / l] % mod * a[m % l] % mod + (n & 1 ? 51 : 21)) % mod * inv32 % mod;
	}
	printf("%llu\n", z);
	return 0;
}

题解

P5678 [GZOI2017]河神

https://www.luogu.com.cn/problem/P5678

题目背景

GZOI2017 D2T1

终于忍受不了苦 X 的搬砖生活, Shlw 把手里的板砖扔进了河里.

不出意料地, 河神冒了出来.

Shlw 说: “我掉了金砖, 快给我金砖!”

“!!! 你已经知道套路了吗,”河神说道, “但是你要金砖的话, 我就不给你2017 彩虹小马大电影的资源了哦. 如果你说实话的话, 我还可以考虑一下.”

Shlw 发现事情并不简单, 在金钱和信仰面前, 难以抉择.

突然, Shlw 不理会河神, 自顾自的地跑走了.

“唉, 现在的年轻人啊... 真不知道在想什么.”Pinkie Pie 感叹, 卸下了河神伪装.

题目描述

Shlw 从河神给的选择中, 获得了一道当年挂掉的代数题的灵感.

但现在他希望你来帮忙解答, 因为他自己忙着去搜小马资源去了.

给出数列 $\{a_n\}$ 和 $\{b_n\}$ 以及 $\{A_n\}$ 的递推关系, 试求出数列 $\{A_n\}$ 第 $N$ 项.

递推关系为:

输入格式

第一行两个正整数 $N$ 和 $K$ 。

第二行 $K$ 个空格隔开的非负整数, 表示 $\{a_n\}$ 。

第三行 $K$ 个空格隔开的非负整数, 表示 $\{b_n\}$ 。

输出格式

一行, 一个整数, 表示 $\{A_n\}$ 。

样例 #1

样例输入 #1

10 5
2 3 5 7 12
23 45 2 4 8

样例输出 #1

提示

【样例解释】

从 $A_0$ 至 $A_{10}$ 分别为: $2, 3, 5, 7, 12, 15, 15, 13, 15, 15, 15$

【数据约束】

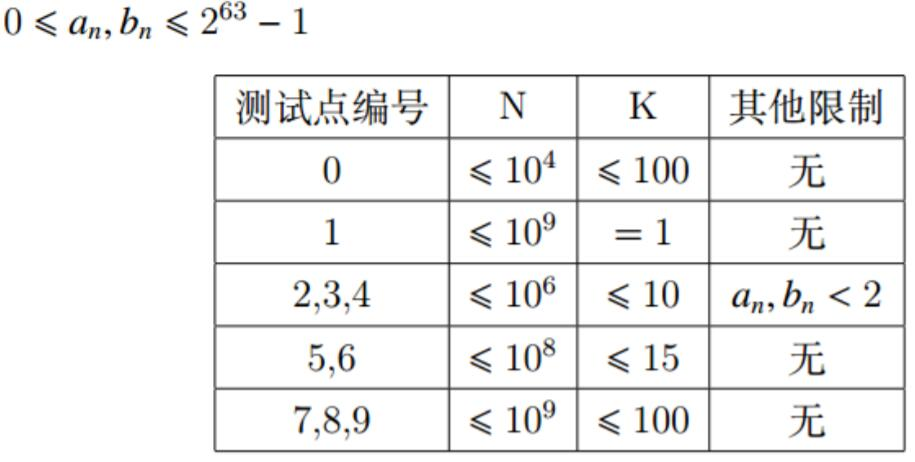
【后记】

后来, Pinkie Pie 偷偷来到 Shlw 家里, 她把这题拿回去考 Apple Jack, 于是 Apple Jack就有了狂吃苹果来畅游多重宇宙的本领.

参考代码

#include <bits/stdc++.h>
using namespace std;
const int p = 1000000007;
long long n;
int m;
long long a[101][101];
long long b[101][101];
void mul(long long a[101][101], long long b[101][101]) {
	long long w[101][101] = {};
	for (int i = 0; i < m; i++) {
		for (int k = 0; k < m; k++) {
			if (a[i][k] == 0) {
				continue;
			}
			for (int j = 0; j < m; j++) {
				w[i][j] |= a[i][k] & b[k][j];
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int main() {
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		cin >> a[0][i];
	}
	for (int i = 0; i < m; i++) {
		cin >> b[i][m - 1];
		if (i > 0)
		{
			b[i][i - 1] = -1;
		}
	}
	for (; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	cout << a[0][0] << endl;
	return 0;
}

题解

a | (b & c)

(a | b) & (a | c)

a & (b | c)

(a & b) | (a & c)

矩阵：二维数组
在计算机比赛中用到的矩阵都是方阵
只有方阵可以做快速幂

为什么矩阵乘法可以出成题？
快速幂 && 取模

哪类题目可以用矩阵乘法
常系数线性齐次递推

为什么矩阵乘法有结合律？
核心是乘法对加法有分配率

f[n + 1] = a f[n] + b g[n] + c h[n]
g[n + 1] = r f[n] + s g[n] + t h[n]
h[n + 1] = x f[n] + y g[n] + z h[n]
转化为类似于这样递推，
多个数组，同时推，n+1结果只和n的结果有关

矩阵加减法对应位置相加减
矩阵乘法不是对应位置相乘

矩阵乘法满足结合律（不一定满足交换律）
可以用快速幂优化
因为取模使得这个方法比暴力效率高很多

零矩阵全是0的矩阵相当于0
零矩阵 * 任意矩阵 = 零矩阵

单位矩阵只有对角线a[i][i]=1的矩阵相当于1
单位矩阵 * 任意矩阵 = 任意矩阵本身

1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

矩阵的0次幂可以认为是单位矩阵

转置矩阵
a[i][j] = b[j][i]

1 2 3
4 5 6
7 8 9
的转置是
1 4 7
2 5 8
3 6 9

a和b互为转置矩阵

(AB)的转置矩阵 = B的转置矩阵 * A的转置矩阵
(AB)的逆矩阵 = B的逆矩阵 * A的逆矩阵

矩阵乘法
95%的情况和快速幂一起用
5%逆矩阵

不要用结构体（除非是非常复杂的矩阵操作）
不要用单位矩阵，尽量减少矩阵乘法的次数
乘法取模尽量快的计算
稀疏矩阵乘法，可以减少乘法次数

易错点，尽量不要涉及到矩阵的负数次方

绝大多数问题都是
矩阵A 乘以矩阵B的n次方

A * B**n

比如 n = 21
A * B * B**4 * B**16

绝大多数问题，A矩阵是一个行向量（只有第一行非0）
很多矩阵乘法是
行向量*矩阵可以优化到 $O(n^2)$ 的矩阵乘法时间复杂度暴力 $O(n^3)$

有时矩阵乘法是
B**t * A
矩阵*列向量可以优化到 $O(n^2)$ 的矩阵乘法时间复杂度暴力 $O(n^3)$

P1962 斐波那契数列

Fibonacci Number
标准定义
f[-2] ...
f[-1] ...
f[0] = 0
f[1] = 1
做法1：

f[n], f[n+1] -> f[n+1], f[n+2] = (f[n+1], f[n] + f[n+1])
f[n], f[n+1] -> f[2n], f[2n+1] =

f[2n] = f[n]f[n+1] + f[n-1]f[n] = f[n] * (f[n+1] + f[n-1]) = f[n] * (f[n+1]2-f[n])
LL F(ll n)
{
if(n==0)
return LL(0,1);
else if(n&1)
{
LL u=F(n-1);
return LL(u.Y,(u.X+u.Y)%p);
}
else
{
LL u=F(n/2);
// u.X = f[n]
// u.Y = f[n+1]
return LL((2u.Y+p-u.X)%pu.X%p,(u.Xu.X+u.Yu.Y)%p);
// f[2n] = (2f[n+1]-f[n]) * f[n];
// f[2n+1] = f[n]*f[n]+f[n+1]*f[n+1];
}
}

gcd(f[n], f[m]) = f[gcd(n, m)];

做法2：
f[i+1] = f[i] + f[i-1]
g[i] = f[i-1]

f[i+1] = f[i] + g[i]
g[i+1] = f[i]

f[i+1] f[i]
0 0

1 1
1 0

(f[i+1]+f[i]) f[i+1]
0 0

=
f[i+2] f[i+1]
0 0

初始知道的是
f[1] f[0]

乘以转移矩阵n次之后得到

f[n+1] f[n]

f[i+1] = a f[i] + b g[i]
g[i+1] = c f[i] + d g[i]

f[i] g[i]
0 0

a c
b d

(a f[i] + b g[i]) (c f[i] + d g[i])
0 0

f[i+1] g[i+1]
0 0

P1349 广义斐波那契数列

https://www.luogu.com.cn/problem/P1349

题目描述

广义的斐波那契数列是指形如 $a_n=p\times a_{n-1}+q\times a_{n-2}$ 的数列。
今给定数列的两系数 $p$ 和 $q$ ，以及数列的最前两项 $a_1$ 和 $a_2$ ，另给出两个整数 $n$ 和 $m$ ，试求数列的第 $n$ 项 $a_n \bmod m$ 。

输入格式

输入包含一行六个整数， $p,q,a_1,a_2,n,m$ 。

输出格式

输出包含一行一个整数表示答案。

样例 #1

样例输入 #1

1 1 1 1 10 7

样例输出 #1

提示

数列第 $10$ 项是 $55$ ， $55 \bmod 7 = 6$ 。

【数据范围】
对于 $100\%$ 的数据， $p,q,a_1,a_2 \in [0,2^{31}-1]$ ， $1\le n,m \le 2^{31}-1$ 。

参考代码

#include <bits/stdc++.h>
using namespace std;
int p = 100000000;
void mul(int a[2][2], int b[2][2]) {
	int w[2][2] = {};
	for (int i = 0; i < 2; i++) {
		for (int j = 0; j < 2; j++) {
			for (int k = 0; k < 2; k++) {
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int main() {
	int a[2][2] = {};
	int b[2][2] = {};
	int n;
	b[1][0] = 1;
	cin >> b[1][1] >> b[0][1] >> a[0][0] >> a[0][1] >> n >> p;
	for (n--; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	cout << a[0][0] << endl;
}

题解

f[i+1] f[i]
0 0

p 1
q 0

(pf[i+1]+qf[i]) f[i+1]
0 0

=
f[i+2] f[i+1]
0 0

初始知道的是
AT start, we know
f[2] f[1]

乘以转移矩阵n-1次之后得到
After multiplied by the transition matrix n-1 times
f[n+1] f[n]

f[2] f[1] -> f[n+1] f[n]

f[i+1] f[i]
0 0

p 1
q 0

(pf[i+1]+qf[i]) f[i+1]
0 0

=
f[i+2] f[i+1]
0 0

初始知道的是
f[2] f[1]

乘以转移矩阵n-1次之后得到

f[n+1] f[n]

f[2] f[1] -> f[n+1] f[n]

必须是常系数线性递推才可以矩阵乘法优化
如果系数中出现了 i 之类的，就不能矩阵乘法优化
f[i] = i * f[i-1]
阶乘是不能优化的

P1939 【模板】矩阵加速（数列）

https://www.luogu.com.cn/problem/P1939

题目描述

已知一个数列 $a$ ，它满足：

$a_x= \begin{cases} 1 & x \in\{1,2,3\}\\ a_{x-1}+a_{x-3} & x \geq 4 \end{cases}$

求 $a$ 数列的第 $n$ 项对 $10^9+7$ 取余的值。

输入格式

第一行一个整数 $T$ ，表示询问个数。

以下 $T$ 行，每行一个正整数 $n$ 。

输出格式

每行输出一个非负整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

4
9
19

提示

对于 $30\%$ 的数据 $n \leq 100$ ；
对于 $60\%$ 的数据 $n \leq2 \times 10^7$ ；
对于 $100\%$ 的数据 $1 \leq T \leq 100$ ， $1 \leq n \leq 2 \times 10^9$ 。

参考代码

#include <bits/stdc++.h>
using namespace std;
int p = 1000000007;
void mul(int a[3][3], int b[3][3]) {
	int w[3][3] = {};
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 3; j++) {
			for (int k = 0; k < 3; k++) {
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int F(long long n) {
	int a[3][3] = {};
	int b[3][3] = {};
	a[0][1] = a[0][2] = 1;
	b[1][0] = b[2][1] = b[0][2] = b[2][2] = 1;
	for (; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	return a[0][0];
}
int main() {
	int t;
	cin >> t;
	for (int tt = 0; tt < t; tt++) {
		long long n;
		cin >> n;
		cout << F(n) << endl;
	}
	return 0;
}

题解

f[i] = f[i-1] + f[i-3]

f[i] f[i+1] f[i+2]
0    0      0
0    0      0

*

0 0 1
1 0 0
0 1 1

=

f[i+1] f[i+2] (f[i+2]+f[i])
0      0      0
0      0      0

=

f[i+1] f[i+2] f[i+3]
0      0      0
0      0      0

f[1] f[2] f[3]
*
转移矩阵(n-1)次方
=
f[n] f[n+1] f[n+2]


假设f[0]=0
f[0] f[1] f[2] // 0 1 1
*
转移矩阵n次方
=
f[n] f[n+1] f[n+2]

P1707 刷题比赛

https://www.luogu.com.cn/problem/P1707

题目背景

nodgd 是一个喜欢写程序的同学，前不久洛谷 OJ 横空出世，nodgd 同学当然第一时间来到洛谷 OJ 刷题。
于是发生了一系列有趣的事情，他就打算用这些事情来出题恶心大家……

题目描述

洛谷OJ当然算是好地方，nodgd 同学打算和朋友分享一下。于是他就拉上了他的朋友 Ciocio 和 Nicole 两位同学一起刷题。喜欢比赛的他们当然不放过这样一次刷题比赛的机会！

在第 $1$ 天 nodgd,Coicoi,Nicole 都只做了 $1$ 道题。

在第 $2$ 天 nodgd,Coicoi,Nicole 都只做了 $3$ 道题。

他们都有着严格的刷题规则，并且会在每一天都很遵守规则的刷一定量的题。

1、nodgd 同学第 $k+2$ 天刷题数量
$a_{k+2}=pa_{k+1}+qa_k+b_{k+1}+c_{k+1}+rk^2+tk+1$

2、Ciocio 同学第 $k+2$ 天刷题数量
$b_{k+2}=ub_{k+1}+vb_k+a_{k+1}+c_{k+1}+w^k$

3、Nicole 同学第 $k+2$ 天刷题数量
$c_{k+2} = xc_{k+1}+yc_k + a_{k+1} + b_{k+1} + z^k+k+2$

（以上的字母 $p,q,r,t,u,v,w,x,y,z$ 都是给定的常数，并保证是正整数）

于是他们开始了长时间的刷题比赛！一共进行了 $n$ 天

但是时间是可贵的，nodgd 想快速知道第 $n$ 天每个人的刷题数量。
不过 nodgd 同学还有大量的数学竞赛题、物理竞赛题、英语竞赛题、美术竞赛题、体育竞赛题…… 要做，就拜托你来帮他算算了。

由于结果很大，输出结果 $\bmod \space m$ 的值即可。

输入格式

第一行两个正整数 $n,m$ 。

第二行四个正整数 $p,q,r,t$ 。

第三行三个正整数 $u,v,w$ 。

第四行三个正整数 $x,y,z$ 。

输出格式

共三行，每行一个名字 + 一个空格 + 一个整数。
依次是 nodgd,Ciocio,Nicole 和他们在第 $n$ 天刷题数量 $\bmod \space m$ 的值。

样例 #1

样例输入 #1

样例输出 #1

nodgd 74
Ciocio 80
Nicole 59

提示

对于 $100\%$ 的数据， $4\le n \le 10^{16}$ ， $2\le m \le 10^{16}$ ， $1\le p,q,r,t,u,v,w,x,y,z \le 100$ 。

参考代码

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n, mod;
ll mul(ll x, ll y)
{
	ll re = 0;
	for (; y > 0; y >>= 9)
	{
		re = (re + y % 512 * x) % mod;
		x = x * 512 % mod;
	}
	return re;
}
void mul(ll a[11][11], ll b[11][11]) {
	ll w[11][11] = {};
	for (int i = 0; i < 11; i++) {
		for (int k = 0; k < 11; k++) {
			if (a[i][k] == 0) {
				continue;
			}
			for (int j = 0; j < 11; j++) {
				w[i][j] = (w[i][j] + mul(a[i][k], b[k][j])) % mod;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int main() {
	int p, q, r, t, u, v, w, x, y, z;
	cin >> n >> mod;
	cin >> p >> q >> r >> t;
	cin >> u >> v >> w;
	cin >> x >> y >> z;
	ll a[11][11] = {
		{3,1,3,1,3,1,w,z,1,1,1}
	};
	ll b[11][11] = {
		{p,1,1,0,1,0,0,0,0,0,0},
		{q,0,0,0,0,0,0,0,0,0,0},
		{1,0,u,1,1,0,0,0,0,0,0},
		{0,0,v,0,0,0,0,0,0,0,0},
		{1,0,1,0,x,1,0,0,0,0,0},
		{0,0,0,0,y,0,0,0,0,0,0},
		{0,0,1,0,0,0,w,0,0,0,0},
		{0,0,0,0,1,0,0,z,0,0,0},
		{r,0,0,0,0,0,0,0,1,0,0},
		{t,0,0,0,1,0,0,0,2,1,0},
		{1,0,0,0,2,0,0,0,1,1,1}
	};
	for (n -= 2; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	printf("nodgd %lld\n", a[0][0]);
	printf("Ciocio %lld\n", a[0][2]);
	printf("Nicole %lld\n", a[0][4]);
	return 0;
}

题解

k*k k 1
0 0 0
0 0 0

1 0 0
2 1 0
1 1 1

(k+1)*(k+1) (k+1) 1
0 0 0
0 0 0

a[2] a[1] b[2] b[1] c[2] c[1] w z 1 1 1

a[k+1] a[k] b[k+1] b[k] c[k+1] c[k] w**k z**k k*k k 1

*

p 1 1 0 1 0 0 0 0 0 0
q 0 0 0 0 0 0 0 0 0 0
1 0 u 1 1 0 0 0 0 0 0
0 0 v 0 0 0 0 0 0 0 0
1 0 1 0 x 1 0 0 0 0 0
0 0 0 0 y 0 0 0 0 0 0
0 0 1 0 0 0 w 0 0 0 0
0 0 0 0 1 0 0 z 0 0 0
r 0 0 0 0 0 0 0 1 0 0
t 0 0 0 1 0 0 0 2 1 0
1 0 0 0 2 0 0 0 1 1 1

=

a[k+2] a[k+1] b[k+2] b[k+1] c[k+2] c[k+1] w**(k+1) z**(k+1) (k+1)*(k+1) (k+1) 1


a[k+2] =

P2044 [NOI2012] 随机数生成器

https://www.luogu.com.cn/problem/P2044

题目描述

栋栋最近迷上了随机算法，而随机数是生成随机算法的基础。栋栋准备使用线性同余法（Linear Congruential Method）来生成一个随机数列，这种方法需要设置四个非负整数参数 $m,a,c,X_0$ ，按照下面的公式生成出一系列随机数 $\{X_n\}$ ：
$X_{n+1}=(aX_n +c)\bmod m$

其中 $\bmod m$ 表示前面的数除以 $m$ 的余数。从这个式子可以看出，这个序列的下一个数总是由上一个数生成的。

用这种方法生成的序列具有随机序列的性质，因此这种方法被广泛地使用，包括常用的 C++ 和 Pascal 的产生随机数的库函数使用的也是这种方法。

栋栋知道这样产生的序列具有良好的随机性，不过心急的他仍然想尽快知道 $X_n$ 是多少。由于栋栋需要的随机数是 $0,1,\dots,g-1$ 之间的，他需要将 $X_n$ 除以 $g$ 取余得到他想要的数，即 $X_n \bmod g$ ，你只需要告诉栋栋他想要的数 $X_n \bmod g$ 是多少就可以了。

输入格式

一行 $6$ 个用空格分割的整数 $m,a,c,X_0,n$ 和 $g$ ，其中 $a,c,X_0$ 是非负整数， $m,n,g$ 是正整数。

输出格式

输出一个数，即 $X_n \bmod g$ 。

样例 #1

样例输入 #1

11 8 7 1 5 3

样例输出 #1

提示

计算得 $X_n=X_5=8$ ，故 $(X_n \bmod g) = (8 \bmod 3) = 2$ 。

对于 $100\%$ 的数据， $n,m,a,c,X_0\leq 10^{18}$ ， $1\leq g\leq 10^8$ ， $n,m\geq 1$ ， $a,c,X_0\geq 0$ 。

参考代码

题解

x[n] c

a 0
1 1

x[n+1] c

另一个做法

设
x[n + 1] = a x[n] + c
a[1] = a
c[1] = c

x[n + m] = a[m] x[n] + c[m]
问a[n] c[n]怎么求

x[n + m] = a[m] x[n] + c[m]
if m % 2 == 1:
x[n + m] = a[1] * x[n + m - 1] + c[1]
x[n + m] = a[1] * (a[m - 1] * x[n] + c[m - 1]) + c[1]
x[n + m] = a[1] * a[m - 1] * x[n] + (a[1] * c[m - 1] + c[1])
a[m] = a[1] * a[m - 1]
c[m] = a[1] * c[m - 1] + c[1]
else:
x[n + m] = a[m/2] (a[m/2] x[n] + c[m/2]) + c[m/2]
x[n + m] = a[m/2] * a[m/2] * x[n] + a[m/2] * c[m/2] + c[m/2]
a[m] = a[m/2] * a[m/2]
c[m] = a[m/2] * c[m/2] + c[m/2]

x[n] = a[m] x[0] + c[m]

等比数列求和怎么做？
公式？涉及到除法，逆元，公比是1
编程中一般用快速幂/倍增

等比数列求和
// S(n, r) == 1 + r + r2 + ... + r(n-1)

int S(int n, int r)
{
if (n == 0)
{
return 0;
}
if (n % 2 == 1)
{
return 1 + S(n - 1, r) * r;
}
else
{
return (1 + r) * S(n / 2, r * r);
}
}

P2461 [SDOI2008] 递归数列

https://www.luogu.com.cn/problem/P2461

题目描述

一个由自然数组成的数列按下式定义：

对于 $i \le k$ ： $a_{i}= b_{i}$ 。

对于 $i > k$ ： $a_{i}= \sum_{j=1}^{k}{c_{j} \times a_{i-j}}$ 。

其中 $b_{1\dots k}$ 和 $c_{1\dots k}$ 是给定的自然数。

写一个程序，给定自然数 $m \le n$ ，计算 $\left( \sum_{i=m}^{n}{a_{i}} \right) \bmod p$ 。

输入格式

第一行一个自然数 $k$ 。

第二行 $k$ 个自然数 $b_{1},b_{2},\dots,b_{k}$ 。

第三行 $k$ 个自然数 $c_{1},c_{2},\dots,c_{k}$ 。

第四行三个自然数 $m,n,p$ 。

输出格式

一行一个正整数，表示 $\sum_{i=m}^{n}{a_{i}} \mod p$ 的值。

样例 #1

样例输入 #1

2
1 1
1 1
2 10 1000003

样例输出 #1

提示

对于 $20\%$ 的数据， $n \le 10^{6}$ 。

对于另外 $30\%$ 的数据， $k=1$ 。

对于 $100\%$ 的数据， $1 \le k \le 15$ ， $1 \le m \le n \le 10^{18}$ ， $0 \le b_{i},c_{i} \le 10^{9}$ ， $p \le 10^{8}$ 。

参考代码

#include <bits/stdc++.h>
using namespace std;
long long L, R;
int m, p;
int b[20];
int c[20];
void mul(int a[20][20], int b[20][20]) {
	int w[20][20] = {};
	for (int i = 0; i < m; i++) {
		for (int k = 0; k < m; k++) {
			if (a[i][k] == 0) {
				continue;
			}
			for (int j = 0; j < m; j++) {
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int F(long long n) {
	int a[20][20] = {};
	int b[20][20] = {};
	b[0][0] = 1;
	for (int i = 1; i < m; i++) {
		a[0][i] = ::b[i];
		b[i][i-1] = 1;
		b[m-i][m-1] = ::c[i];
	}
	for (; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	return a[0][0];
}
int main() {
	cin >> m;
	m++;
	for (int i = 1; i < m; i++) {
		cin >> b[i];
	}
	for (int i = 1; i < m; i++) {
		cin >> c[i];
	}
	cin >> L >> R >> p;
	cout << (F(R) - F(L-1) + p) % p << endl;
	return 0;
}

题解

s[0] = 0;
s[n] = a[1] + a[2] + .. + a[n]

s[n] a[n+1] a[n+2] a[n+3]

1 0 0 0
1 0 0 c3
0 1 0 c2
0 0 1 c1

s[n+1] a[n+2] a[n+3] a[n+4]

初始
s[0] a[1] a[2] a[3]
乘以n次转移矩阵，得到
s[n] ....

Error: ENOENT: no such file or directory, open '/Users/wwwwodddd/Dropbox/Github/Informatics/solutions/problems/P4910.md'

0 -> 2
1 -> 1

Lucas Numbers

n=0 2
n=1 1
n=2 3
n=3 4
n=4 7
n=5 11

f[0] = 0
f[1] = 1
f[2] = 1
f[3] = 2
f[4] = 3
f[5] = 5
f[6] = 8

l[n] = f[n+1] + f[n-1]

P1357 花园

https://www.luogu.com.cn/problem/P1357

题目描述

小 L 有一座环形花园，沿花园的顺时针方向，他把各个花圃编号为 $1 \sim n$ 。花园 $1$ 和 $n$ 是相邻的。

他的环形花园每天都会换一个新花样，但他的花园都不外乎一个规则：任意相邻 $m$ 个花圃中都只有不超过 $k$ 个 C 形的花圃，其余花圃均为 P 形的花圃。

例如，若 $n=10$ , $m=5$ , $k=3$ ，则

CCPCPPPPCC 是一种不符合规则的花圃。
CCPPPPCPCP 是一种符合规则的花圃。

请帮小 L 求出符合规则的花园种数对 $10^9+7$ 取模的结果。

输入格式

只有一行三个整数，分别表示 $n, m, k$ 。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

10 5 3

样例输出 #1

样例 #2

样例输入 #2

6 2 1

样例输出 #2

提示

数据规模与约定

对于 $40\%$ 的数据，保证 $n \le 20$ 。
对于 $60\%$ 的数据，保证 $m=2$ 。
对于 $80\%$ 的数据，保证 $n \le 10^5$ ；
对于 $100\%$ 的数据，保证 $2 \leq n \le 10^{15}$ ， $2 \leq m \leq \min(n, 5)$ ， $1 \leq k \lt m$ 。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int p = 1000000007;
long long n;
int m, l, sz, z;
int a[32][32];
int b[32][32];
void mul(int a[32][32], int b[32][32]) {
	int w[32][32] = {};
	for (int i = 0; i < sz; i++) {
		for (int k = 0; k < sz; k++) {
			if (a[i][k] == 0) {
				continue;
			}
			for (int j = 0; j < sz; j++) {
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int main() {
	cin >> n >> m >> l;
	sz = 1 << m;
	for (int i = 0; i < sz; i++)
	{
		if (__builtin_popcount(i) <= l)
		{
			a[i][i] = 1;
			int j = i >> 1;
			if (__builtin_popcount(j) <= l)
			{
				b[i][j] = 1;
			}
			j |= 1 << m - 1;
			if (__builtin_popcount(j) <= l)
			{
				b[i][j] = 1;
			}
		}
	}
	for (; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	for (int i = 0; i < sz; i++)
	{
		z = (z + a[i][i]) % p;
	}
	cout << z << endl;
	return 0;
}

题解

CCPPP PCPCPCCPPP

A * B ** 19
A * B * (B ** 18)
A * B * ((B * B) ** 9)

求出

n=5 ~ n=100 的答案
假设这个题目是线性递推数列
f[i] = a[1] * f[i-1] + a[2] * f[i-2] + ... + a[t] * f[i-t]
直接解方程，去解递推的系数a[i]

找到递推系数之后，就可以使用矩阵乘法或多项式取模来解决这个问题了

P5004 专心OI - 跳房子

https://www.luogu.com.cn/problem/P5004

题目背景

Imakf 有一天参加了 PINO2017 PJ 组，他突然看见最后一道题：

他十分蒟蒻，写不出来。

而如今他还是一个蒟蒻，他又看见一道题：

他还是写不出来，于是便来请教您。

题目描述

您有 $N$ 个格子，排成一行，从左往右编号为 $1,2,\cdots,N$ 。您站在 $1$ 号格子的左边无限远，开始从左往右跳，跳到 $N$ 号格子右侧为止。由于您是一位成功的 OIer，您自然长得很胖，所以您的腿部力量也非常大！这使得您跳一次，当前格子到目标格子中间必须至少空出来 $M$ 格，但您可以跳无数格远！

您认为这么跳太没意思了，于是便想计算出有多少种方案可以跳完全程。由于方案可能过多，您会输出方案数量模 $(10^9+7)$ 的值

方案不同当且仅当经过的任一一个格子编号不同。

输入格式

第一行两个整数 $N,M$ 。

输出格式

一个整数，表示跳完全程的方案模 $(10^9+7)$ 。

样例 #1

样例输入 #1

5 1

样例输出 #1

样例 #2

样例输入 #2

6 2

样例输出 #2

提示

测试数据编号	$N$	$M$
$1,2$	$\leq10$	$=1$
$3,4$	$\leq10^7$	$=1$
$5,6$	$\leq10^6$	$=2$
$7,8$	$\leq10^5$	$=3$
$9,10$	$\leq10^4$	$=5$
$11,12$	$\leq10^{12}$	$=1$
$13,14$	$\leq10^{18}$	$=10$
$15\sim20$	$\leq10^{18}$	$=15$

对于 $100\%$ 的数据，满足 $1 \le N \le 10^{18}$ 。

样例一

luogu

样例二

luogu

绿色格子为您站在上面过的格子。

参考代码

#include <bits/stdc++.h>
using namespace std;
const int p = 1000000007;
long long n;
int m;
int a[20][20];
int b[20][20];
void mul(int a[20][20], int b[20][20]) {
	int w[20][20] = {};
	for (int i = 0; i < m; i++) {
		for (int k = 0; k < m; k++) {
			if (a[i][k] == 0) {
				continue;
			}
			for (int j = 0; j < m; j++) {
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int main() {
	cin >> n >> m;
	for (int i = 0; i < m; i++) {
		a[0][i] = i + 1;
		b[i+1][i] = 1;
	}
	b[0][m] = b[m][m] = 1;
	a[0][m] = m + 1;
	m++;
	for (; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	printf("%d\n", a[0][0]);
	return 0;
}

题解

f[i] 最后一步落在i的方案数
f[i] = sum(j < i - M, f[j])
s[i] = f[1] + f[2] + ... + f[i]
f[i] = s[i-M-1]
s[i] = s[i-1] + f[i]
其实不需要维护f？

s[i] = s[i-1] + s[i - M - 1]

s[0] = 1 ''
s[1] = 2 o x
s[2] = 3 oo xo ox
s[3] = 5 ooo xoo oxo oox xox
s[4] = 8
s[5] = 13

i <= M; s[i] = i + 1

s[0] = 1
s[1] = 2
s[2] = 3
s[3] = 4
s[4] = 6
s[5] = 9
s[6] = 13

s[i] s[i+1] ... s[i+M]

0 0 0 0 1
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 1

s[i+1] s[i+2] ... s[i+M+1] = s[i] + s[i+M]

s[0] .....

s[n] .....

f[0] + f[1] + ... + f[n] = f[n+2] - 1

P3746 [六省联考 2017] 组合数问题

https://www.luogu.com.cn/problem/P3746

题目描述

组合数 $C_n^m$ 表示的是从 $n$ 个互不相同的物品中选出 $m$ 个物品的方案数。举个例子，从 $(1, 2, 3)$ 三个物品中选择两个物品可以有 $(1, 2)$ ， $(1, 3)$ ， $(2, 3)$ 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 $C_n^m$ 的一般公式：

$C_n^m = \frac {n!} {m! \ (n - m)!}$

其中 $n! = 1 \times 2 \times \cdots \times n$ 。（特别地，当 $n = 0$ 时， $n! = 1$ ；当 $m > n$ 时， $C_n^m = 0$ 。）

小葱在 NOIP 的时候学习了 $C_i^j$ 和 $k$ 的倍数关系，现在他想更进一步，研究更多关于组合数的性质。小葱发现， $C_i^j$ 是否是 $k$ 的倍数，取决于 $C_i^j \bmod k$ 是否等于 $0$ ，这个神奇的性质引发了小葱对 $\mathrm{mod}$ 运算（取余数运算）的兴趣。现在小葱选择了是四个整数 $n, p, k, r$ ，他希望知道

$\left( \sum_{i = 0}^\infty C_{nk}^{ik + r} \right) \bmod p,$

即

$\left( C_{nk}^{r} + C_{nk}^{k + r} + C_{nk}^{2k + r} + \cdots + C_{nk}^{(n - 1)k + r} + C_{nk}^{nk + r} + \cdots \right) \bmod p$

的值。

输入格式

第一行有四个整数 $n, p, k, r$ ，所有整数含义见问题描述。

输出格式

一行一个整数代表答案。

样例 #1

样例输入 #1

2 10007 2 0

样例输出 #1

样例 #2

样例输入 #2

20 10007 20 0

样例输出 #2

提示

对于 $30\%$ 的测试点， $1 \leq n, k \leq 30$ ， $p$ 是质数；
对于另外 $5\%$ 的测试点， $p = 2$ ；
对于另外 $5\%$ 的测试点， $k = 1$ ；
对于另外 $10\%$ 的测试点， $k = 2$ ；
对于另外 $15\%$ 的测试点， $1 \leq n \leq 10^3, 1 \leq k \leq 50$ ， $p$ 是质数；
对于另外 $15\%$ 的测试点， $1 \leq n \times k \leq 10^6$ ， $p$ 是质数；
对于另外 $10\%$ 的测试点， $1 \leq n \leq 10^9, 1 \leq k \leq 50$ ， $p$ 是质数；
对于 $100\%$ 的测试点， $1 \leq n \leq 10^9, 0 \leq r < k \leq 50, 2 \leq p \leq 2^{30} - 1$ 。

参考代码

#include <bits/stdc++.h>
using namespace std;
long long n;
int p, m, r;
int a[50][50];
int b[50][50];
void mul(int a[50][50], int b[50][50]) {
	int w[50][50] = {};
	for (int i = 0; i < m; i++) {
		for (int k = 0; k < m; k++) {
			if (a[i][k] == 0) {
				continue;
			}
			for (int j = 0; j < m; j++) {
				w[i][j] = (w[i][j] + (long long)a[i][k] * b[k][j]) % p;
			}
		}
	}
	memcpy(a, w, sizeof w);
}
int main() {
	cin >> n >> p >> m >> r;
	n *= m;
	a[0][0] = 1;
	for (int i = 0; i < m; i++)
	{
		b[i][i]++;
		b[i][(i+1) % m]++;
	}
	for (; n > 0; n >>= 1) {
		if (n & 1) {
			mul(a, b);
		}
		mul(b, b);
	}
	cout << a[0][r] << endl;
	return 0;
}

题解

C(n, r) = C(n - 1, r) + C(n - 1, r - 1)

f[0][0] = 1
f[0][1] = 0
..
f[0][k-1] = 0

f[i][j] = sum(任意t, C(i, tk + j)) = sum(任意t, C(i - 1, tk + j) + C(i - 1, tk + j - 1))
sum(任意t, C(i - 1, tk + j)) + sum(C(i - 1, tk + j - 1))
f[i][j] = f[i - 1][j] + f[i - 1][(j - 1) % k]

1 0 0
1 1 0
1 2 1
2 3 3
5 5 6
11 10 11

f[0] f[1] f[2] f[3] f[4]

1 1 0 0 0
0 1 1 0 0
0 0 1 1 0
0 0 0 1 1
1 0 0 0 1

f[0]+f[4] f[0]+f[1] f[1]+f[2] f[2]+f[3] f[3]+f[4]

P4599 [HEOI2012]赵州桥

https://www.luogu.com.cn/problem/P4599

题目背景

fyg 背着他的电脑来到河北省来，就是为了见一眼古老的赵州桥。

终于，他来到了赵州桥，放下了电脑，正准备休息。一阵风吹来，从中闪现出一人影。 fyg 只觉天昏地暗，待得再次睁开眼时，发觉自己已经到了一神奇的国度，置身于一巨大的圆盘之上。放眼看去，四周都是奇形怪状的桥，不远处有一老头盘膝而坐。

题目描述

fyg 还沉浸在惊奇之中，老头（难道就是传说中走过赵州桥的张老头！！）便开口了：凡人，你现在在我的世界中，想要出去就要回答我的问题。fyg 只得点头，老头继续道：你现在要去闯关，我给你 $m$ 种颜色，总共有 $n$ 关（神仙也懂数学，表示压力巨大。。==）。每一关中有一座桥，在第 $i$ 关中，桥长度有 $i$ 个单位，每个单位长度上有 $2$ 个格子（也就是说这座桥有 $2i$ 个格子），现在你要计算出：在这座桥上涂色使得桥上相邻格子的颜色不一样总方案数，然后再乘上 $(2\times i)^m$ 。如在第 $1$ 关，若你手上有 $2$ 种颜色，分别为蓝色和绿色。则总方案数为 $2\times 2\times 2=8$ 种，涂色方案数为 2（如下图，旋转、翻转相同算不同的方案），然后还要再乘 2 个 2，最后你出来之后我会问你所有关中计算出来的数的和。如果你能答对，我就可以让你出去了，否则就无限轮回吧。

fyg 表示这个问题太水了，完全不想算。。。于是，他马上打开电脑上了QQ找到了喜欢计算的你，求你帮他直接把最终答案算出来，让他回到赵州桥上。

这两个数都有可能很大，fyg 不想为难你，所以你只要告诉他其除以 $p$ 的余数。

输入格式

只有一行，其中包含三个正数 $n$ 、 $m$ 、 $p$ ，分别由一个空格分开。 $n$ 、 $m$ 、 $p$ 含义和题目描述一致。

输出格式

一行，表示方案数的和除以 $p$ 的余数。

样例 #1

样例输入 #1

2 5 50

样例输出 #1

提示

【样例说明】
总共有 $2$ 关。

第一关的桥长度为 $1$ ，总共有 $2$ 个格子，涂色方案数为 $20$ ，再乘上 $2 ^ 5$ ，第一关中计算出的数为 $640$ 。

第二关的桥长度为 $2$ ，总共有 $4$ 个格子，涂色方案数为 $260$ ，再乘上 $4 ^ 5$ ，第二关中计算出的数为 $266240$ 。

两个数字加起来除以 $50$ 余 $30$ ，故输出为 $30$ 。

【数据范围】

对于其中 25%的数据，满足 $n\leq10^6$ ， $m\leq200$ ， $p\leq10^9$ ；

对于其中 40%的数据，满足 $n\leq10^9$ ， $m\leq120$ ， $p\leq10^9$ ；

对于其中 15%的数据，满足 $n\leq10^9$ ， $m\leq200$ ， $p \leq10^9$ ；

对于最后 20%的数据，满足 $n\leq10^9$ ， $m\leq3000$ ， $p\leq3000$ ；

HEOI 2012 Day2 Task1

参考代码

题解

如何用矩阵乘法，计算1到n的k次方和

(1k+2k+...+(i-1)k) i0 i1 i2 i3 ... ik

...

(1k+2k+...+i**k) (i+1)**0 (i+1)**1 (i+1)**2 (i+1)**3 ... (i+1)**k

k = 4

1 0 0 0 0 0
0 1 1 1 1 1
0 0 1 2 3 4
0 0 0 1 3 6
0 0 0 0 1 4
1 0 0 0 0 1

如何用矩阵乘法，计算1到n的k次方和

(......) i0*ri i1*ri i2*ri i3*ri ... ik*ri

...

(......+ik*ri) r*(i+1)0*r(i+1) (i+1)1*r(i+1) (i+1)2*r(i+1) (i+1)3*r(i+1) ... (i+1)k*r(i+1)

k = 5

1 0 0 0 0 0
0 1r 1r 1r 1r 1r
0 0 1r 2r 3r 4r
0 0 0 1r 3r 6r
0 0 0 0 1r 4r
1 0 0 0 0 1r

bzoj 3157
bzoj 3516
等比数列 * 等差数列（一次多项式）
等比数列 * 多项式（m次多项式）
时间复杂度O(m^2)

在计算过程中只做了一次除法，比如除以n，但是n在模mod下没有逆元，怎么办？
之前对mod取模

之后对(mod*n)取模
最后直接除以n即可，应当能整除

只做了一次除法常见的情况：
FWT / Burnside

bzoj 3157: 国王奇遇记

3516: 国王奇遇记加强版

逆矩阵

f[i+1] f[i]
0 0

1 1
1 0

(f[i+1]+f[i]) f[i+1]
0 0

0 1
1 -1

f[i+1] f[i]
0 0

1 1
1 0
*
0 1
1 -1

1 0
0 1

如果A矩阵乘以B矩阵等于单位矩阵
那么A矩阵和B矩阵互为逆矩阵

1 1 1 0
1 0 0 1

做行初等变换
1.交换某两行
2.将某一行的所有元素乘上k(k \neq 0)
3.将某一行的所有元素乘上k加到另一行去

1 1 1 0
1 0 0 1

1 0 0 1
1 1 1 0

1 0 0 1
0 1 1 -1

行初等变换
交换两行
同一行乘以一个数字k
第i行减去第j行对应的位置

在要求逆的矩阵 A 后面接一个单位矩阵 I
对于这个 n 行 2n 列的矩阵，做行初等变换
使得前 n 列变成单位矩阵，后 n 列就是求逆的结果

高斯消元求逆矩阵
枚举第i行：
a[i][i] 可能是 0
找第j行，使得a[j][i] != 0
交换第i行和第j行（必须让a[i][i]不为0）
第i行同时乘以 a[i][i] 的逆元（让a[i][i]变成1
将所有不是第i行的第j行，减去若干倍的第i行，使得a[j][i]变成0

取模加const会变快
比如 / 10

429496729 / 4294967296
如果模数在编译时不知道，但是输入之后不会改变

#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ull;
typedef __uint128_t L;
struct FastMod {
    ull b, m;
    FastMod(ull b) : b(b), m(ull((L(1) << 64) / b)) {}
    ull reduce(ull a) {
        ull q = (ull)((L(m) * a) >> 64);
        ull r = a - q * b; // can be proven that 0 <= r < 2*b
        return r >= b ? r - b : r;
    }
}FM(2);
int main()
{
    FM = FastMod(1000000007);
    cout << FM.reduce(1000000000000000000) << endl;
    return 0;
}

高斯消元解方程
a11x1 + a12x2 + a13x3 == b1
a21x1 + a22x2 + a23x3 == b2
a31x1 + a32x2 + a33*x3 == b3

已知所有的a和b，求x
nn的矩阵A * n1的列向量x = n*1的列向量b

求出A矩阵的逆矩阵A^(-1)
x = A^(-1) * b

b数组直接记在a矩阵的后面一列

P6009 [USACO20JAN]Non-Decreasing Subsequences P

第一反应，区间维护a[i][j]表示区间内以i开始，以j结束的不下降子序列个数
区间支持合并，可以线段树
超时
加了一堆常数优化，发现还是超时

已有a[i][j]表示一个数组的答案，在这个数组之后加了一个x，答案会怎么变？
已有a[i][j]表示一个数组的答案，删掉了数组中最后一个数字x，答案会怎么变？

已有a[i][j]表示一个数组的答案，删掉了数组中第一个数字x，答案会怎么变？

很多计数的动态规划，是可逆的

K = 5
x = 4

大部分位置不变
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1

原本1开始i(i<=4)结束的序列，现在可以变成1开始，x结束的序列

f[4]=
1 0 0 1 0
0 1 0 1 0
0 0 1 1 0
0 0 0 2 0
0 0 0 0 1

newa[1][x] = a[1][1] + a[1][2] + ... + a[1][x]
newa[2][x] = a[2][1] + a[2][2] + ... + a[2][x]
newa[3][x] = a[3][1] + a[3][2] + ... + a[3][x]

g[4]=
1 0 0 -1/2 0
0 1 0 -1/2 0
0 0 1 -1/2 0
0 0 0 1/2 0
0 0 0 0 1

f[x] 和 g[x] 互为逆矩阵，f[x]*g[x] = g[x]*f[x] = I

可以求转移矩阵的前缀乘积，和逆矩阵的前缀乘积

inv(AB) = inv(B)*inv(A)
inv(B)*inv(A) * A * B = inv(B)*B = I
(inv(B)inv(A)) * (AB) = I

空串：E=
1 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0

最终(l, r)的答案 =
E * f[a[l]] * f[a[l+1]] * f[a[l+2]] * ... * f[a[r]] =
E * (g[a[l-1]] * g[a[l-2]] * ... * g[a[1]]) * (f[a[1]] * f[a[2]] * ... * f[a[l-1]] * f[a[l]] * f[a[l+1]] * f[a[l+2]] * ... * f[a[r]])
= E * q[l-1] * p[r]

p[i] = f[a[1]] * f[a[2]] * ... * f[a[i]]
q[i] = g[a[i]] * ... * g[a[2]] * g[a[1]]

sp[r][i] = p[r][i][0] + p[r][i][1] + ... + p[r][i][k-1] (第i行的和)

最终(l, r)的答案 =
q[l-1] * p[r] 第一行的和
既然只关注第一行的值，那么就只计算第一行
for (int i = 0; i < m; i++)
{
for (int j = 0; j < m; j++)
{
ans = (ans + (long long)q[l][0][i] * p[r][i][j]) % mod;
}
}

ans = 0
for (int i = 0; i < m; i++)
{
ans = (ans + (long long)q[l][0][i] * sp[r][i]) % mod;
}

总时间复杂度
预处理：O(n * k^2)
每个询问：O(k)
总复杂度：O(n * k^2 + q * k)

行列式值为0的矩阵，没有逆矩阵
如果转移矩阵的行列式值为0，那么说明有一些列是没有用的

多个初始值的矩阵乘法
可以放在初始矩阵的不同行，节约一些时间。

0 1 Fibonacci Number f[i] = f[i-1] + f[i-2]
2 1 Lucas Number l[i] = l[i-1] + l[i-2]
*
0 1
1 1

1 1
1 3

1 2
3 4

2 3
4 7

3 5
7 11

这个方法和快速幂时，记录下矩阵的1次幂，2次幂，4次幂，8次幂……等价。
矩阵乘法最慢的部分，是将转移矩阵自己平方

P1827 [USACO3.4]美国血统 American Heritage